Qualunque sistema anche non fisico ha bisogno, per prevederne la sua evoluzione, di un modello matematico che ci consende di calcolarne le variazioni temporali delle sue caratteristiche principali. Ma ha anche bisogno che siano note le sue condizioni iniziali, da cui partire col calcolo, che, come abbiamo visto, si basa su equazioni. Normalmente piccole variazioni iniziali portano a piccole variazioni nell'evoluzione di un sistema. Se faccio cadere a terra un bicchiere, ha poca importanza se cade da un certo punto o da un punto ad esso vicino...
Non è così per tutta una classe di sistemi che chiamiamo caotici, in cui piccole variazioni dei parametri iniziali portano a grandi variazioni della sua evoluzione temporale.
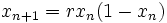
Questa equazione rappresenta un modello demografico e descrive due effetti:
- riproduzione, in cui la popolazione cresce a un tasso proporzionale alla popolazione corrente quando la popolazione iniziale è piccola;
- mortalità, in cui il tasso di crescita diminuisce con una velocità proporzionale al valore ottenuto prendendo la "portata" teorica dell'ambiente meno la popolazione corrente.
in essa
- xn è un numero compreso tra zero e uno, e rappresenta il rapporto tra la popolazione esistente e quella massima possibile in un anno n, e quindi xorappresenta il rapporto tra la popolazione iniziale (all'anno 0) e quella massima
- r è un numero positivo, e rappresenta un tasso combinato tra la riproduzione e la mortalità.
- La sensibilità alle condizioni iniziali è comunemente nota come "effetto farfalla", effetto così chiamato per via del titolo di una relazione presentata da Edward Lorenz nel 1972 all'Associazione Americana per l'Avanzamento della Scienza a Washington, DC, dal titolo La prevedibilità: Il battere delle ali di una farfalla in Brasile provoca un tornado in Texas?.[4] Il movimento delle ali di una farfalla rappresenta un piccolo cambiamento nella condizione iniziale del sistema, che provoca una catena di eventi che portano a fenomeni di scala sempre più vasta. Se la farfalla non avesse sbattuto le ali, la traiettoria del sistema sarebbe stata molto diversa.
- Molti fenomeni hanno comportamenti caotici: ad esempio quelli metereologici,in climatologia, fluidodinamica (turbolenza), teoria del laser, ecologia.
- Qualche sistema dinamico, come la mappa logisticache abbiamo visto all'inizio, mostra comportamenti caotici che si estendono in tuttospazio delle configurazioni (si chiama anche transitività topologica), tuttavia è possibile che l'andamento caotico sia confinato solo in certe regioni di esso. Il caso di maggior interesse sorge quando un largo insieme delle configurazioni iniziali tende a convergere in una delimitata regione di spazio, l'attrattore, dove avvengono fenomeni caotici.
- Attrattore di Lorentz
-
- Attrattore di Lorentz e metereologia

