Una delle tante maniere di dimostrare tale teorema è questa:
Sembra una cosa innocente ed ovvia, legata al nostro senso comune. Ma contiene in sè alcune premesse nientaffatto ovvie: che lo spazio sia piatto ed infinito. Se neghiamo una o tutte e due queste premesse, possono accadere cose molto strane ad esempio:
- la somma degli angoli interni di un triangolo non sia uguale a 180º
- che da un punto esterno ad una retta non ci siano parallele(geometria ellittica) alla retta o ce ne siano infinite (iperbolica)
Del resto la geometria euclidea aveva dentro di sè un vulnus: il quinto postulato (per un punto esterno ad una retta esiste una sola parallela alla retta data), che era indecidibile all'interno della stessa geometria euclidea (teorema o postulato?)
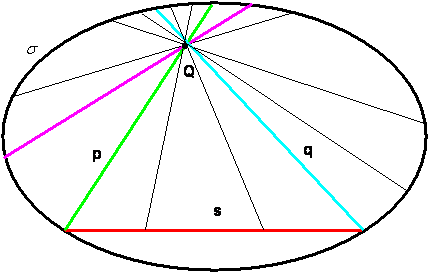
Geometria iperbolica:
al minimo due, ma anche infinite parallele. In questo caso, se suppongo che lo spazio sia limitato da una curva chiusa, le rette sono corde e datao un punto esterno ad una corda, ci stanno infinite corde che non intersecano la corda data!
Geometria ellittica:
sulla sfera, invece, non esistono parallele, in quanto le rette sono i cerchi massimi!

Voi direte: "che masturbazione mentale!" E invece no. La teoria della gravitazione di Einstein presuppone una geometria non euclidea, di tipo ellittico, come vedremo.

