2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,…
Sembrano irregolari? In realtà non lo sono ed è proprio questo che bisogna dimostrare, Qual è la distribuzione dei numeri primi, qual è la legge che lega i numeri primi su i numeri naturali???
Proprio questo è il KERNEL dell’ ipotesi di Riemann, infatti egli ipotizzò che i numeri primi per quanto possano essere irregolari non lo sono.
Vediamo come :
Riemann utilizzo la funzione zeta di Eulero nel campo dei numeri complessi.
Risultava dunque possibile dare un valore alla funzione zeta in corrispondenza di qualunque numero complesso, in modo da poter disegnare il grafico di una funzione che coprisse tutto il piano complesso.
La funzione zeta di Eulero utilizzata da Riemann.
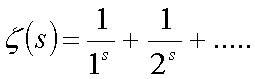
Il tutto lo possiamo scrivere come :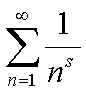
con s appartenete alla classe dei numeri complessi
Il problema era dunque conoscere la distribuzione degli zeri della funzione zeta e vedere dove si presentassero.Riemann decise di calcolare alcuni dei punti a per vedere con precisione dove si trovassero.
“Quando cominciò ad analizzare l’esatta collocazione di questi punti, ebbe una grossa sorpresa. Invece di essere sparpagliati qua e là su tutto il piano, gli zeri che calcolava sembravano disporsi sul piano complesso su una linea retta con parte reale uguale a ½”.
Ovviamente, siccome la funzione zeta ha infiniti zeri, Riemann non poté calcolarli tutti. Anzi, ne calcolò solo una piccola quantità. Tuttavia si convinse di una cosa: tutti gli zeri della funzione zeta sarebbero caduti lungo la retta.
Questa è dunque la congettura di Riemann.
(se questa ipotesi e’ vera, il problema dei numeri primi e’ risolto)

