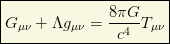A scuola, tutti abbiamo studiato che da un punto esterno a una retta si può condurre un’unica parallela passante per quel punto: è il quinto postulato di Euclide, noto come il “postulato delle parallele”, una delle premesse essenziali per costruire tutta la geometria, com’è riportata nei suoi Elementi (terzo secolo A. C.), il libro che viene considerato la Bibbia dei matematici.
E se qualcuno affermasse che per questo punto esterno alla retta si possono condurre due o più rette parallele o nessuna, diremmo che è impazzito. Eppure questi nuovi postulati, sostitutivi di quello euclideo, sono perfettamente legittimi, ma ci vollero più di duemila anni perché qualcuno osasse esprimere queste idee, all’origine delle geometrie non euclidee.
E’ opinione comune infatti che due rette sono parallele se, prolungate, non si incontrano mai, come i binari del treno. Ma questa idea di “non incontrarsi mai” presuppone che le rette proseguano all’infinito ed è stato proprio l’infinito, che ha creato il maggior imbarazzo nella storia della matematica. Per questo, nel corso dei secoli, molti grandi matematici hanno tentato invano di eliminare il postulato delle parallele, con una dimostrazione che consentisse di trasformarlo in teorema, togliendolo così dalla posizione imbarazzante di premessa fondamentale della matematica. Si tentò anche di introdurre postulati sostitutivi, per dimostrare che qualsiasi altro postulato avrebbe portato a inevitabili contraddizioni e che, in conclusione, l’unico possibile era quello di Euclide. Ma non emerse alcuna contraddizione, anzi le deduzioni che se ne traevano, risultavano in molti casi perfettamente legittime.
I principali protagonisti della grande avventura matematica che portò alla creazione delle geometrie non euclidee, quelle appunto che non ammettono il quinto postulato, sono Carl Friedrich Gauss (1777 – 1855), Nikolaj Ivanovich Lobačevskij (1793 – 1856) e János Bolyai (1802 – 1860).
Gauss, considerato da molti il più grande matematico della storia, fu il primo a convincersi della validità delle geometrie emerse dai nuovi postulati e fu lui a battezzarle “geometrie non euclidee”. Scriveva a un amico, nel 1824, che i suoi studi lo avevano portato “a una curiosa geometria, piuttosto diversa dalla nostra, ma fortemente coerente, che ho sviluppato con grande soddisfazione”. Ma non pubblicò nulla sull’argomento, nel timore delle critiche e incomprensioni dei suoi colleghi, che avrebbero potuto screditarlo.
Saranno Lobačevskij e Bolyai, due matematici che vivevano ai margini del mondo accademico tradizionale, a trovare il coraggio di pubblicare i primi lavori di geometria non euclidea, a dimostrazione del fatto che una nuova idea nasce più facilmente al di fuori dell’ambiente ufficiale, più restio ad abbandonare i vecchi e radicati concetti. Lobačevskij, che viveva nella lontana Kazan’, ai piedi degli Urali, prima docente e poi rettore della locale università, scrisse un lavoro, nel 1826, su quella che definì la “geometria immaginaria”, lavoro che non solo non riuscì a pubblicare, ma che andò anche perduto. Nel 1830, riuscì finalmente a far pubblicare i suoi studi su una rivista russa. Si tratta del primo lavoro pubblicato sull’argomento e questo gli dà il diritto di essere considerato il fondatore della geometria non euclidea. Di Lobačevskij Renato Betti, docente di geometria del Politecnico di Milano, presenta ora un’accurata biografia, Lobačevskij – L’invenzione delle geometrie non euclidee. Betti riporta sia i risultati ottenuti da Lobačevskij e dagli altri matematici dell’epoca, sia la sua vita e le vicende nella Russia della prima metà dell'800. “Da una parte c’è funzionario scrupoloso e attento ai valori correnti del suo tempo – scrive Betti - dall'altra un ricercatore teso all'innovazione, che non ferma le proprie concezioni davanti alle convenzioni ed allo stile dominanti. Bravo studente, ma non il migliore. Bravo docente, ma gli vengono preferiti altri per essere mandati all'estero. Era sicuramente mosso da una certa inquietudine intellettuale, ma questo non gli impedisce in un paio di occasioni giovanili di farsi strumento di repressione nei confronti dei colleghi.
Il personaggio più simpatico, fra i padri delle geometrie non euclidee, è sicuramente Bolyai, ufficiale dell’esercito austro – ungarico, violinista di gran talento, che teneva concerti a Vienna e in altre capitali europee, ballerino impareggiabile, rubacuori e grande spadaccino. I suoi biografi raccontano che, in una sola giornata, sfidò a duello tredici ufficiali, suoi compagni d'arme, e riuscì a vincer tutti, suonando il violino tra un duello e l'altro per tenere la sua mano in esercizio, e sicuramente anche per impressionare gli avversari. Bolyai, che nel libro di Betti non trova molto spazio e che lo obbliga, speriamo, ad una nuova biografia, era figlio di un matematico amico di Gauss, ed era ufficiale di stanza a Temesvár, dove incominciò ad occuparsi della nuova geometria per combattere la noia del servizio militare. Inutilmente il padre, quando lo venne a sapere, gli scrisse: "Figlio mio, ti imploro, desisti dal tuo tentativo. Il problema delle parallele è cosa da temere e da evitare, quanto le passioni dei sensi, poiché anch'esso può rubarti tutto il tuo tempo e privarti della salute, della serenità di spirito e della felicità". In realtà le geometrie non euclidee lo portarono ad una crisi profonda e ad abbandonare, per un certo periodo, lo studio della matematica, quando scoprì che era stato preceduto da Lobačevskij che non conosceva. I suoi primi lavori sulla “geometria assoluta”, come aveva battezzato la sua geometria, uscirono infatti nel 1833, tre anni dopo il primo libro di Lobačevskij, in modo del tutto indipendente, ma facendogli perdere il primato della scoperta. Questo nulla toglie al merito suo e di Lobačevskij di aver avviato una grande rivoluzione culturale. “La fine del dominio della geometria euclidea – scrive Morris Kline – segnò la fine del dominio di ogni verità assoluta”. E’ una rivoluzione paragonabile a quella copernicana o a quella darwiniana, che ogni persona di cultura dovrebbe conoscere, partendo proprio dallo studio di Renato Betti.
Federico Peiretti, LA STAMPA, 2 luglio 2005
Renato Betti
Lobačevskij. L’invenzione delle geometrie non euclidee
Bruno Mondadori


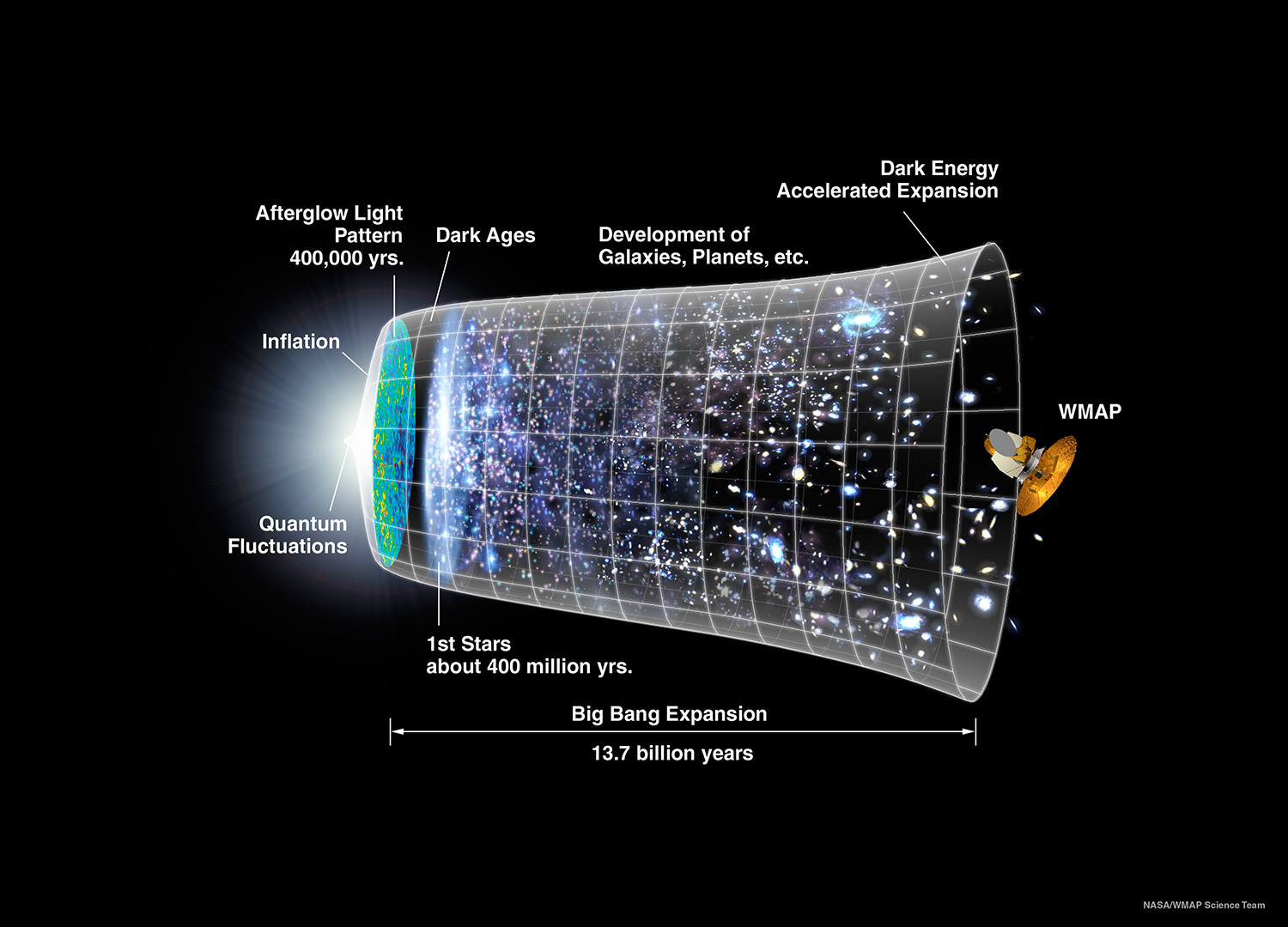
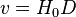 .Queste due formule ci dicono che z, spostamento verso il rosso della luce delle stelle è proporzionale alla loro distanza ed anche la velocità con cui si allontanano tali stelle. In altre parole stelle lontane hanno un colore, per noi, non più bianco, ma che tende a non essere visibile. La maggior parte delle stelle è lontana da noi, non ci illumina, non illumina quella parte di cosmo che vediamo. Quindi il cielo ci appare nero perchè quello che vediamo è poco illuminato ed, in più, la luce si diffonde in uno spazio che aumenta sempre più velocemente.
.Queste due formule ci dicono che z, spostamento verso il rosso della luce delle stelle è proporzionale alla loro distanza ed anche la velocità con cui si allontanano tali stelle. In altre parole stelle lontane hanno un colore, per noi, non più bianco, ma che tende a non essere visibile. La maggior parte delle stelle è lontana da noi, non ci illumina, non illumina quella parte di cosmo che vediamo. Quindi il cielo ci appare nero perchè quello che vediamo è poco illuminato ed, in più, la luce si diffonde in uno spazio che aumenta sempre più velocemente.

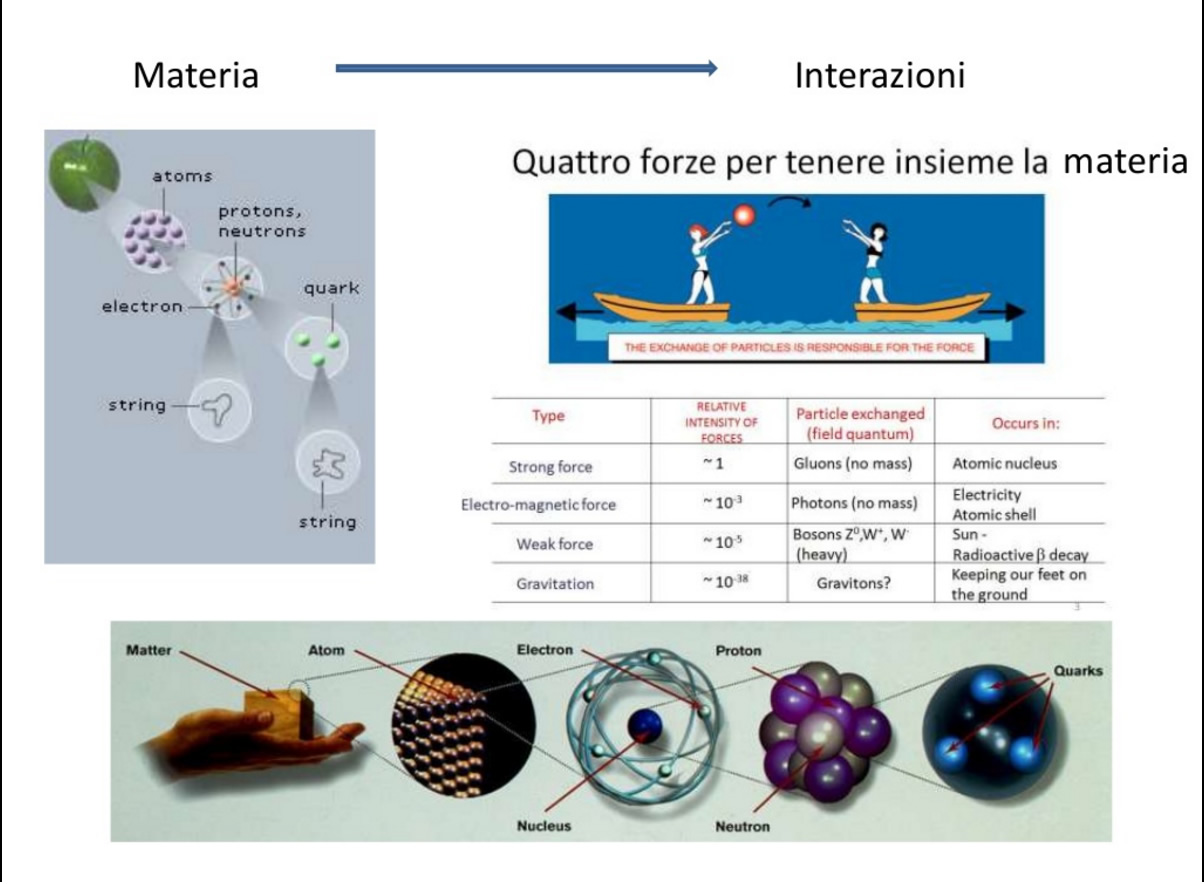
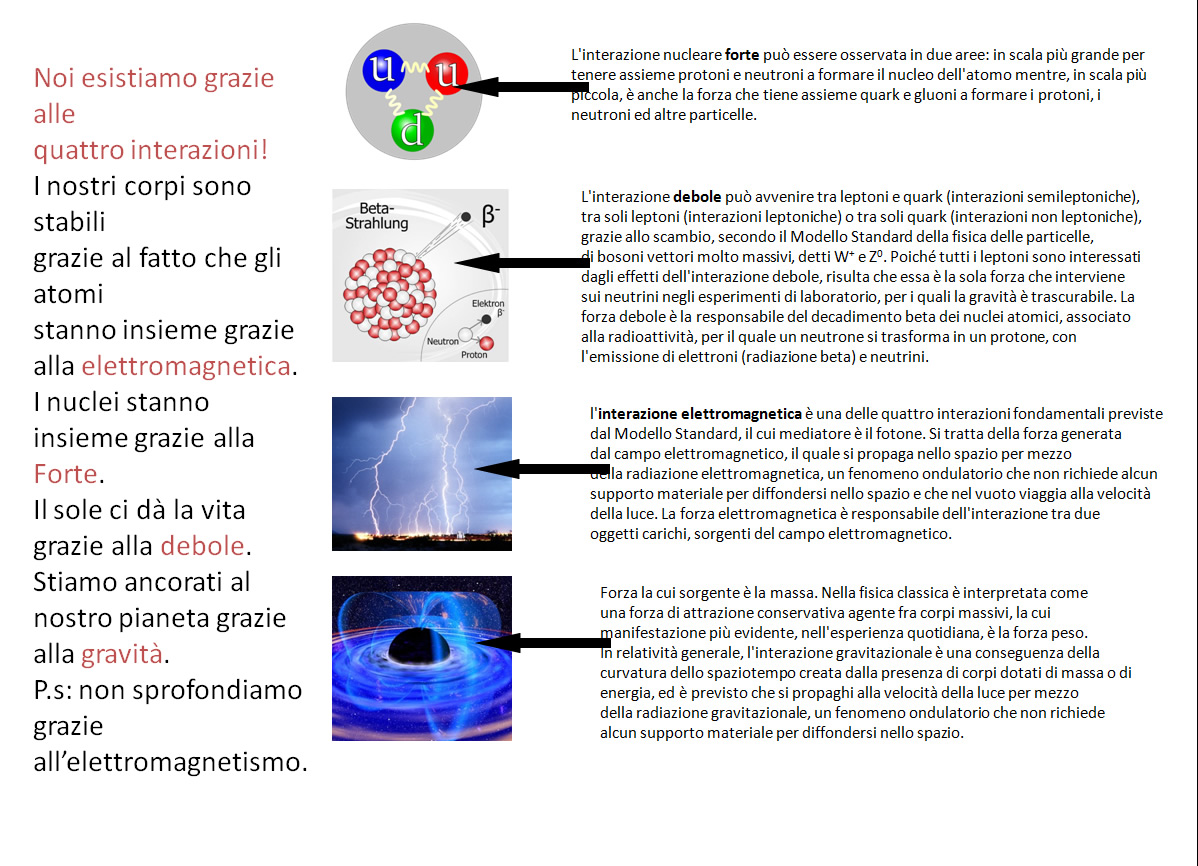
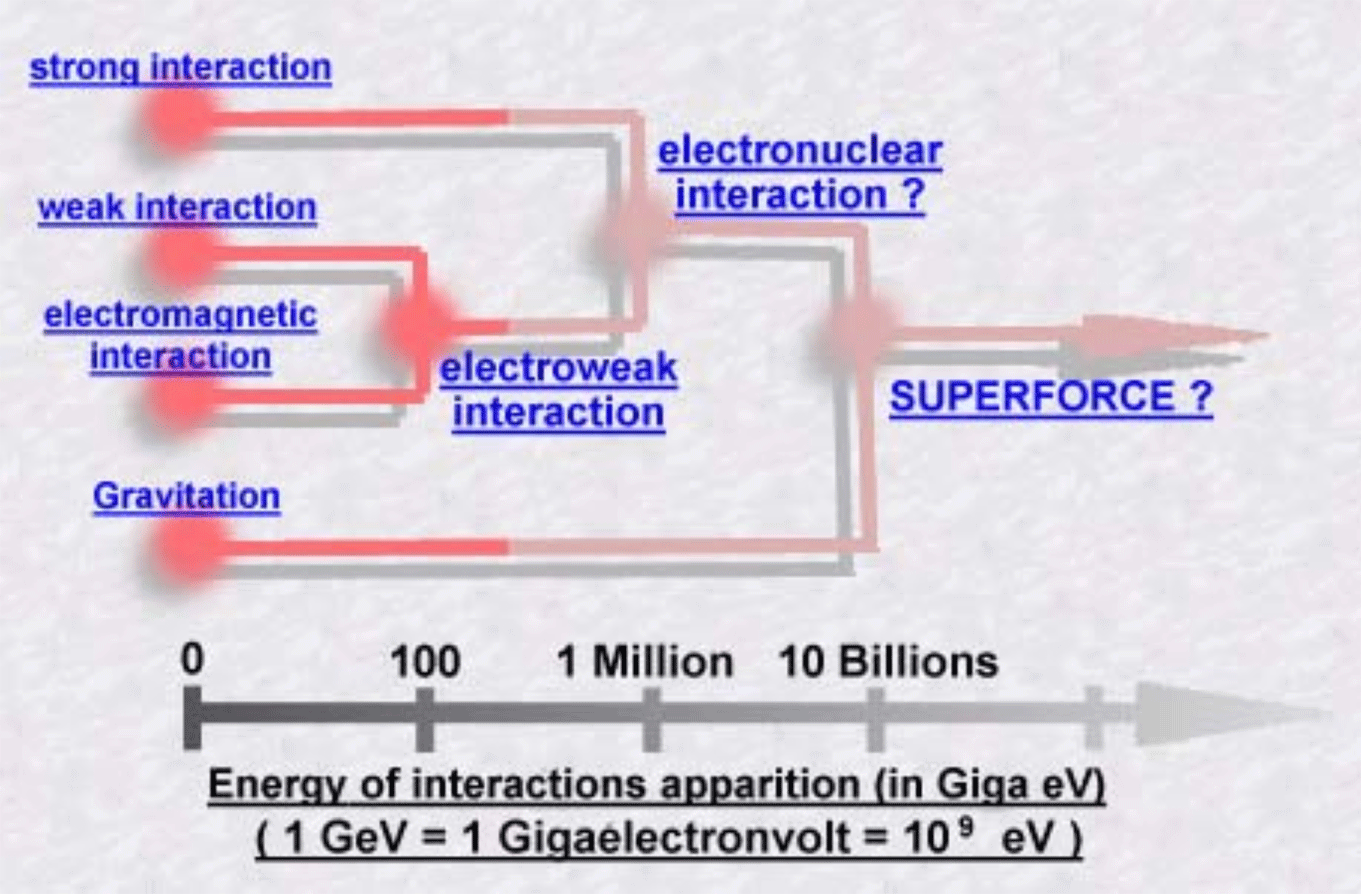 Nell'immagine successiva sono evidenziate le forze coinvolte e la loro evoluzione, o meglio la loro separazione man mano che l'universo si espandeva, fino ad arrivare ai giorni nostri. Come si può notare, la forza di gravità è la prima a formarsi ed è anche la più debole delle altre tre. La verifica sperimentale di tali fenomeni è, in linea di principio, fattibile. L'HLC di Ginevra è un primo banco di prova, ma c'è da dire che, malgrado sia la macchina più potente mai costruita, le energie che mette in gioco sono molto lontane da quelle necessarie per notare il processo di unificazione delle forze
Nell'immagine successiva sono evidenziate le forze coinvolte e la loro evoluzione, o meglio la loro separazione man mano che l'universo si espandeva, fino ad arrivare ai giorni nostri. Come si può notare, la forza di gravità è la prima a formarsi ed è anche la più debole delle altre tre. La verifica sperimentale di tali fenomeni è, in linea di principio, fattibile. L'HLC di Ginevra è un primo banco di prova, ma c'è da dire che, malgrado sia la macchina più potente mai costruita, le energie che mette in gioco sono molto lontane da quelle necessarie per notare il processo di unificazione delle forze